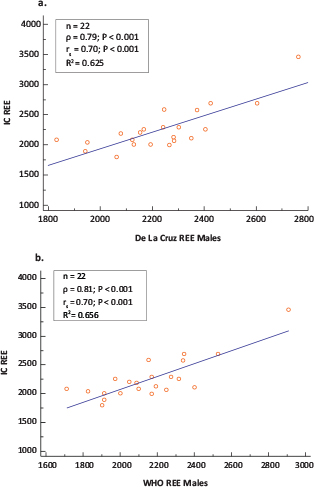
FIG 1. Scatter Plots and Correlation coefficients (ρ =Pearson’s coefficient; rs =Spearman’s Rank Order Coefficient) of Measured Versus Predicted REE Using (a) IC and the De La Cruz and (b) IC and WHO Equations in Males (n = 22).
Original Research
Leila Itani, Hana Tannir, Dima Kreidieh, Dana El Masri and Marwan El Ghoch
Department of Nutrition and Dietetics, Faculty of Health Sciences, Beirut Arab University, P.O. Box 11-5020 Riad El Solh, Beirut, Lebanon
The quantification of resting energy expenditure (REE) in patients with obesity is an important measure. We aimed to evaluate the validity of predictive equations in estimating REE compared with indirect calorimetry (IC) in treatment-seeking Arab adults with overweight or obesity. Twenty-three predictive equations were compared with REE values measured by IC (Vmax Encore 229) in 89 adult participants with overweight or obesity (mean age = 40.62 ± 15.96 years and mean body mass index [BMI] = 35.02 ± 4.60 kg/m2) referred to the Department of Nutrition and Dietetics of Beirut Arab University (Lebanon). The accuracy of the predictive equations was evaluated on the basis of whether the percentage prediction was within 10% of the measured REE, and the mean difference between predicted and measured values (bias). The Bland–Altman method was used to assess the agreement between the predicted and measured values. The equations that demonstrated the closest agreement with IC were the De La Cruz equation in males (accurate predictions: 68.2%; bias: −19.52 kcal/day) and the Mifflin equation in females (accurate prediction: 61.2%; bias: −36.43 kcal/day). In conclusion, we suggest that these two equations produce the least biased estimations for REE in this population.
Keywords: obesity; resting energy expenditure; indirect calorimetry; predictive equations
Obesity is an alarming health condition associated with physical and psychosocial comorbidities,1,2 impaired health-related quality of life3 and an increased rate of mortality worldwide.4 The same scenario is also present in Arabic-speaking countries, where a significant proportion of citizens5 are heavily affected by obesity or are overweight, particularly in Kuwait, Egypt, UAE, Bahrain, Jordan and Saudi Arabia.6,7
Total energy expenditure in humans is determined by the resting energy expenditure (REE), dietary-induced thermogenesis and energy expenditure due to physical activity, and in sedentary people (i.e. in cases of obesity), REE represents the major fraction (≈ 60–70%).8 During weight management programmes, REE assessment in patients with overweight or obesity is crucial, since this permits an accurate quantification of the energy necessary to optimise weight loss and weight-loss maintenance in a later phase.9
The most widely accepted method of measuring REE is indirect calorimetry (IC).10–12 However, some important limitations of this technique include the requirements for skilled technicians and sophisticated instrumentation, and its time-consuming nature. As a result, this technique is not available in standard clinical settings.13 Consequently, several predictive equations aiming to estimate REE have been validated and are now widely used by clinicians as an alternative to IC measurement,14 even though the accuracy of some of these equations is still controversial for patients with overweight or obesity and their use is a matter of debate in this population.15 Moreover, many of these equations have been validated for individuals in Western society,14,16 and to the best of our knowledge, very few have been validated for individuals from Arab-speaking countries.17
These considerations prompted us to assess the accuracy and validity of 23 REE predictive equations when compared to IC, which is considered a validated tool for this purpose, in treatment-seeking Arab adults with overweight or obesity.
Eighty-nine participants with overweight or obesity of both genders actively seeking weight-loss treatment were recruited consecutively after referral by general practitioners to the Nutritional and Weight Management Outpatient Clinic—Collaborating Centre for Obesity Management (COM) affiliated with The European Association for the Study of Obesity (EASO)—in the Department of Nutrition and Dietetics of Beirut Arab University (BAU) in Lebanon from May 2017 to August 2019. The sample size was determined a priori assuming a moderate effect size of 0.3 (Cohen’s d) and 80% power with 95% CI. The eligibility criteria were as follows: age ≥18 years, body mass index (BMI) ≥25.0 kg/m2 and at least one of the following comorbidities: type 2 diabetes, cardiovascular disease, sleep apnoea, severe joint disease or two or more risk factors. No specific exclusion criteria were applied except pregnancy or lactation, medication that is known to influence body weight or composition, or any clinical condition that contraindicated weight loss. The study obtained the approval of the Institutional Review Board of BAU (No. 2017H-0034-HS-R-0241), and all participants gave informed written consent for the use of their anonymous personal data.
Body weight was measured by trained dieticians using an electronic weighing scale (SECA 2730-ASTRA, Germany). Height was measured using a stadiometer. The BMI was then calculated according to the standard formula.
The REE was measured in the morning using a Vmax Encore 229 SensorMedics system. This determines the exhaled minute volume based on the air dilution method and features variable flow that can be adjusted to maintain the fraction of expired carbon dioxide between 0.5 and 1.0%. An infrared gas analyser was used to measure carbon dioxide concentrations in expired and inspired air, while a galvanic fuel cell was used to measure oxygen concentrations. Gas sensors were calibrated with two gas mixtures, and the exhaled air was collected in a rigid plastic canopy.18 Following a 12-hour fast, participants rested supine in a quiet, darkened room for 30 minutes before VO2 and VCO2 were measured for 20 minutes, the last 15 minutes of which were also used to determine REE. In addition, 22 popular and less popular predictive equations were used to estimate REE based on age, gender, height and weight, as indicated.19–41
Body composition was measured using a segmental body composition analyser (BC-418, Tanita Corp., Tokyo, Japan).42 After the gender, age and height information had been entered into the device, participants were asked to stand in a stable position in bare feet. The device provided separate body mass readings for different segments of the body, using an algorithm incorporating impedance, age and height to estimate the total and regional fat mass (FM) and free fat mass (FFM).42
Descriptive statistics are presented as means and standard deviations (SD). The normality of the data was checked using Kolmogorov–Smirnov tests, as well as Quantile–Quantile and normal probability plots. The Bland–Altman method was used to assess the agreement between the predicted and measured REE by IC. Initially, Pearson’s product moment correlation43 and the Spearman’s rank order correlation coefficient were calculated to assess the strength of association between the measured and predicted REE. A scatter plot of the measured (y) and the predicted (x) REE was drawn, and R2 was calculated. A paired sample t-test was used to evaluate whether or not the means of the differences between the values obtained by the IC measurement and each equation were significantly different from zero.43 The mean difference between the predicted REE and measured REE (bias) was considered a measure of accuracy on a group level.44 The average percentage difference between the measured and predicted (predicted–measured)/measured × 100) was calculated, and agreement was defined at ±10%.27,45 The percentage of individuals that had a predicted REE within ±10% of the measured REE was considered a measure of accuracy at an individual level.44 A prediction between 90 and 110% of the measured REE was considered an accurate prediction; a prediction <90% of the measured REE was classified as an under-prediction and a prediction >110% of the measured REE was classified as an over-prediction.44 The normality of bias was checked using Kolmogorov–Smirnov tests, and the limits of agreement (LoA) were calculated for a 95% CI as the mean difference ±1.96 × SD of the bias. The proportional bias was assessed by ordinary least square regression (OLS) of the bias on the mean of the two methods ([predicted + measured]/2) on the differences44 and calculated as the percentage error (the limit of agreement divided by the mean IC REE multiplied by 100).44 A systematic error is confirmed if the line of equality in the Bland–Altman plot lies outside the 95% CI of the bias (bias ± critical value for paired t-test × Standard error of the mean [SEM]). Agreement between measured and predicted REE is confirmed if the bias falls between ±10% (LoA). Statistical significance was set at P < 0.05. All statistical analyses were carried out using SPSS version 25.0 (IBM Corp., Armonk, NY, USA). MedCalc version 19.1 software was used to plot the linear regression and Bland–Altman plots and to calculate the LoA.45
Table 1 shows the data for the 89 participants (females, n = 67, 75.3%), summarising mean age, BMI, FM, FM%, FFM respiratory quotient (RQ) and REE measured by means of IC.
In males, two equations demonstrated the closest agreement when compared with the IC measure of REE, namely the De La Cruz29 and World Health Organization (WHO)40 equations, but did not completely conform within the a priori set criteria of 10% acceptable bias. This is indicated by the 68.2% accurate prediction of both equations with 32% of the observations falling beyond this criterion. The mean REE from the De La Cruz and WHO equations were 2,236 ± 212 kcal/day and 2,161 ± 263 kcal/day, respectively, which were comparable to a measured REE of 2,256 ± 363 kcal/day (Table 2). The bias between the REE values estimated using the De La Cruz29 and WHO equations40 and those measured using IC were not significantly different from zero (Table 2). De La Cruz underestimated IC on average by 19.52 ± 234.41 kcal/day, while the WHO equation underestimated on average by 93.81 ± 214.89 kcal/day (Table 2). The least maximum and minimum percentage bias were for the De La Cruz (−20.08 and 14.88%) and the WHO equations (−17.61 and 14.09%) with the lowest mean percentage bias for De La Cruz (−0.22 ± 9.38%) as compared to WHO (−3.39 ± 8.86%) (Table 2). The precision of the bias for De La Cruz (95% CI: −123.46; 84.41) and WHO (95% CI: −189.09; 1.46) equations indicated no systematic bias. However, although both equations showed a strong correlation with the measured REE (Figure 1a and 1b), both equations showed proportional bias, as illustrated by the slope and intercept of the ordinary least squares (OLS) regression of the bias on the mean of the two methods and the Bland–Altman plot (Figure 2a and 2b). The proportional bias for the De La Cruz and WHO equations indicates a tendency towards underestimation with increasing measured IC and overestimation with decreasing measured IC, although the majority of the predicted values will lie within the a priori set limits (Figure 2a and 2b). The LoA exceeded the 10% set criteria, as reflected by a percentage error of 40.7 and 37.4% for De La Cruz and WHO, respectively (Figure 2a and 2b), which is equivalent to almost double the a priori set limits. Although the LoA indicates that 95% of samples predicted by these equations will lie between limits exceeding the a priori set criteria of 10% (Table 2), most of the predicted values (68.2%) in this study were within 10% of the measured REE with the least percentage error and mean percentage bias and least prediction error for the De La Cruz equation. Although Harris Benedict’s equation showed the highest accuracy on the individual level, it demonstrated a higher percentage bias on the group level with a higher tendency towards under-prediction of IC measured REE and systematic bias. The remaining 21 equations exceeded the a priori set criteria as reflected by the LoA and percentage error.
| Equation | REE (kcal/day) | Mean difference (bias) | 95% CI of bias (precision) | Pearson’s correlation | % bias | Minimum % bias | Maximum % bias | N (%) Under-prediction1 | N (%) Accurate prediction2 | N (%) Over-prediction3 | % error | Lower LoA | Upper LoA | Effect size | P-value4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Indirect calorimetry | 2,256 ± 363 | - | - | - | - | - | - | - | - | - | - | - | ||||
| 1. | Harris Benedict | 2,114 ± 272 | −141.69 ± 206.42 | −233.21; −50.17 | 0.826 | −5.66 ± 7.96 | −20.18 | 5.01 | 6 (27.3) | 16 (72.7) | 0 (0.0) | 35.867 | −546.28 | 262.89 | −0.69 | 0.004 |
| 2. | WHO | 2,162 ± 263 | −93.81 ± 214.89 | −189.09; 1.46 | 0.810 | −3.39 ± 8.86 | −17.61 | 14.09 | 6 (27.3) | 15 (68.2) | 1 (4.5) | 37.366 | −515.00 | 327.97 | −0.44 | N.S |
| 3. | FAO | 2,149 ± 288 | −106.47 ± 232.66 | −209.62; −3.31 | 0.768 | −4.01 ± 9.97 | −25.19 | 12.33 | 6 (27.3) | 15 (68.2) | 1 (4.5) | 40.427 | −562.48 | 349.55 | −0.46 | 0.044 |
| 4. | Mifflin | 1,777 ± 214 | −478.27 ± 223.08 | −577.18; −379.37 | 0.821 | −20.61 ± 6.65 | −33.84 | −12.04 | 22 (100.0) | 0 (0.0) | 0 (0.0) | 38.762 | −915.50 | −41.04 | −2.14 | <0.001 |
| 5. | Schofield a | 2,139 ± 271 | −116.94 ± 226.29 | −217.28; −16.61 | 0.782 | −4.42 ± 9.44 | −20.58 | 15.32 | 7 (31.8) | 14 (63.6) | 1 (4.5) | 39.320 | −560.47 | 326.58 | −0.52 | 0.024 |
| 6. | Schofield b | 2,127 ± 281 | −128.31 ± 231.10 | −230.78; −25.85 | 0.771 | −4.97 ± 9.74 | −24.63 | 12.66 | 6 (27.3) | 15 (68.2) | 1 (4.5) | 40.155 | −581.26 | 324.63 | −0.56 | 0.017 |
| 7. | Müller a | 1,810 ± 191 | −445.48 ± 228.98 | −547.01; −343.95 | 0.834 | −19.02 ± 6.60 | −33.39 | −10.70 | 22 (100.0) | 0 (0.0) | 0 (0.0) | 39.788 | −894.29 | 3.33 | −1.95 | <0.001 |
| 8. | Müller b | 1,807 ± 201 | −448.87 ± 224.47 | −548.40; −349.35 | 0.833 | −19.22 ± 6.58 | −32.61 | −11.01 | 22 (100.0) | 0 (0.0) | 0 (0.0) | 39.004 | −888.83 | −8.91 | −2.00 | <0.001 |
| 9. | Lorenzo | 2,098 ± 252 | −157.49 ± 208.95 | −250.13; −64.85 | 0.828 | −6.28 ± 7.73 | −21.41 | 3.85 | 7 (31.8) | 15 (68.2) | 0 (0.0) | 36.308 | −567.04 | 252.06 | −0.75 | 0.002 |
| 10. | Korth | 1,896 ± 226 | −360.03 ± 220.17 | −457.64; −262.41 | 0.819 | −15.32 ± 7.05 | −30.05 | −6.47 | 16 (72.7) | 6 (27.3) | 0 (0.0) | 38.256 | −791.55 | 71.50 | −1.64 | <0.001 |
| 11. | Weijs | 1,989 ± 269 | −269.61 ± 216.83 | −365.74; −173.47 | 0.805 | −11.40 ± 7.52 | −26.02 | 0.60 | 10 (45.5) | 15 (54.5) | 0 (0.0) | 37.676 | −694.59 | 155.38 | −1.24 | <0.001 |
| 12. | Frankenfield a | 1,726 ± 174 | −530.15 ± 240.83 | −639.92; −423.37 | 0.822 | −22.75 ± 6.71 | −37.00 | −12.74 | 22 (100.0) | 0 (0.0) | 0 (0.0) | 41.847 | −1002.18 | −58.11 | −2.20 | <0.001 |
| 13. | Frankenfield b | 1,817 ± 193 | −438.95 ± 230.99 | −541.36; −336.53 | 0.824 | −18.73 ± 6.88 | −33.54 | −9.06 | 20 (90.9) | 2 (9.1) | 0 (0.0) | 40.137 | −891.69 | 13.80 | −1.90 | <0.001 |
| 14. | De La Cruz | 2,236 ± 212 | −19.52 ± 234.41 | −123.46; 84.41 | 0.791 | −0.22 ± 9.38 | −20.08 | 14.88 | 3 (13.6) | 15 (68.2) | 4 (18.2) | 40.731 | −478.97 | 439.93 | −0.08 | N.S |
| 15. | Willis | 1,681 ± 207 | −575.06 ± 230.95 | −677.46; −472.66 | 0.806 | −24.92 ± 6.82 | −37.45 | −14.64 | 22 (100.0) | 0 (0.0) | 0 (0.0) | 40.129 | −1027.72 | −122.40 | −2.49 | <0.001 |
| 16. | Huang | 1,748 ± 199 | −508.01 ± 232.37 | −611.04; −404.99 | 0.816 | −21.86 ± 6.38 | −35.96 | −13.21 | 22 (100.0) | 0 (0.0) | 0 (0.0) | 40.376 | −963.45 | −52.57 | −2.19 | <0.001 |
| 17. | De Luis | 2,106 ± 225 | −149.64 ± 267.15 | −268.09; −31.19 | 0.679 | −5.60 ± 10.38 | −26.80 | 13.13 | 8 (36.4) | 13 (59.1) | 1 (4.5) | 46.420 | −673.26 | 373.98 | −0.56 | 0.016 |
| 18. | Rosa | 2,104 ± 261 | −151.58 ± 206.31 | −243.05; −60.11 | 0.830 | −6.06 ± 7.71 | −20.51 | 3.94 | 7 (31.8) | 15 (68.2) | 0 (0.0) | 35.848 | −555.95 | 252.79 | −0.73 | 0.002 |
| 19. | Bernestein | 1,668 ± 260 | −587.70 ± 213.91 | −682.54; −492.86 | 0.813 | −25.77 ± 6.96 | −41.04 | −16.76 | 22 (100.0) | 0 (0.0) | 0 (0.0) | 37.169 | −1006.97 | −168.43 | −2.75 | <0.001 |
| 20. | Owen | 1,946 ± 176 | −309.95 ± 249.61 | −420.62; −199.28 | 0.785 | −12.77 ± 7.81 | −31.55 | −4.16 | 12 (54.5) | 10 (45.5) | 0 (0.0) | 43.372 | −799.193 | 179.29 | −1.24 | <0.001 |
| 21. | Livingston | 1,965 ± 164 | −290.80 ± 253.05 | −403.00; −178.61 | 0.794 | −11.85 ± 8.26 | −31.67 | 0.50 | 12 (54.5) | 10 (45.5) | 0 (0.0) | 43.970 | −786.79 | 205.18 | −1.15 | <0.001 |
| 22. | Lazzer | 2,077 ± 269 | −178.38 ± 210.95 | −271.91; −84.85 | 0.817 | −7.30 ± 7.78 | −22.19 | 3.17 | 8 (36.4) | 14 (63.6) | 0 (0.0) | 36.654 | −591.84 | 235.08 | −0.85 | 0.001 |
| 23. | Ikeda | 1,808 ± 170 | −447.77 ± 240.01 | −554.19; −341.36 | 0.834 | −19.02 ± 6.78 | −35.03 | −10.70 | 22 (100.0) | 0 (0.0) | 0 (0.0) | 41.703 | −918.19 | 22.64 | −1.87 | <0.001 |
CI = confidence interval; FAO= ; LoA = limits of agreement; REE = resting energy expenditure; WHO = World Health Organization. 1Proportion of people with difference from measured REE < 10% indicating under-prediction. 2Proportion of people with difference from measure REE between 90 and 10% indicating accurate prediction. 3Proportion of people with difference form measured REE >10% indicating over-prediction 4P-value for one sample t-test. a and b, superscripts stands for two versions of the equations. |
||||||||||||||||

FIG 1. Scatter Plots and Correlation coefficients (ρ =Pearson’s coefficient; rs =Spearman’s Rank Order Coefficient) of Measured Versus Predicted REE Using (a) IC and the De La Cruz and (b) IC and WHO Equations in Males (n = 22).
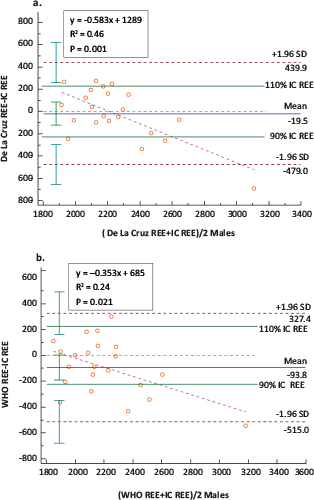
FIG 2. Bland–Altman Plot: Differences in the Measurements of REE Using (a) IC and the De La Cruz and (b) IC and WHO Equations in Males (n = 22).
In females, the prediction ability was lower than in males. However, four equations were in closest agreement when compared with the IC measure of REE, namely Mifflin,21 De La Cruz,29 Willis32 and De Luis,31 but these did conform completely within the a priori set criteria of 10% acceptable bias. The highest prediction accuracy was observed in descending order starting with 61.2% for Mifflin, followed by 56.7% for De La Cruz and Willis. The mean REE from these equations was comparable to the measured REE of 1,710 ± 265 kcal/day with the closest being De La Cruz (1,715 ± 199 kcal/day), followed by Willis (1,706 ± 191 kcal/day), then Mifflin (1,674 ± 175 kcal/day) and lastly, the De Luis (1,698 ± 188 kcal/day) equation (Table 3). The mean bias between the REE values estimated using the Mifflin,21 De La Cruz,29 Willis32 and De Luis31 equations was not significantly different from zero (Table 3). When compared with the measured REE, Mifflin underestimated the IC on average by 36.43 ± 214.73, Willis by 3.90 ± 225.08 and De Luis by 12.17 ± 234.02, while De La Cruz overestimated by 4.51 ± 232.29 kcal/day (Table 3). The least maximum and minimum percentage bias was similar for the four equations, ranging between −31.33 and 33.11%. The mean percentage bias was lowest for De Luis (0.70 ± 13.12%), Mifflin (−0.81 ± 11.90%) and Willis (1.13 ± 12.82%), followed by De La Cruz (1.61 ± 13.12%) (Table 3) (Figure 4a–4d). The precision of the bias indicated no systematic bias for De La Cruz (95% CI: −52.15; 61.17), De Luis (95% CI: −69.25; 44.92), Willis (95% CI: −59.53; 51.74) and Mifflin (95% CI: −88.80; 15.95) (Table 3) (Figure 4a–4d). Although the four equations showed a moderate correlation with the measured REE (Figure 3a–3d), the four equations showed proportional bias, as illustrated by the slope and intercept of the OLS regression of the bias on the means of the two methods (Figure 4a–4d) and the Bland–Altman plot. The proportional bias for the four equations indicates a tendency towards underestimation with increasing measured IC and overestimation with decreasing measured IC. The LoA exceeded the 10% set criteria as reflected by a percentage error ranging from 49.22 to 53.65% with the least being for Mifflin equation (Figure 4a–4d) which is equivalent to almost double the a priori set limits. Although the LoA indicate that 95% of samples predicted with these equations will lie between limits exceeding the a priori set criteria of 10% (Table 3), Mifflin showed the highest percentage (61.2%) of accurate predictions amongst individuals coupled with a low percentage bias (0.81 ± 11.90%) for the group (Table 3). The remaining 19 equations exceeded the 10% set criteria as reflected by the LoA and percentage error of 52.28–53.53% which is equivalent to almost more than double the a priori set limits of 10%.
| Equation | REE (kcal/day) | Mean difference (bias) | 95% CI of bias (precision) | Pearson’s correlation | % bias | Minimum % bias | Maximum % bias | N (%) Under-prediction1 | N (%) Accurate prediction2 | N (%) Over-prediction3 | % error | Lower LoA | Upper LoA | Effect size | P-value4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Indirect calorimetry | 1,710 ± 265 | - | - | - | - | - | - | - | - | - | - | - | ||||
| 1. | Harris Benedict | 1,598 ±152 | −112.39 ± 217.20 | −165.37; −59.42 | 0.572 | −5.21 ± 11.48 | −33.31 | 26.39 | 22 (32.8) | 39 (58.2) | 6 (9.0) | 49.79 | −538.10 | 313.31 | −0.52 | <0.001 |
| 2. | WHO | 1,647 ± 179 | −63.50 ± 231.19 | −119.89; −7.11 | 0.514 | −2.31 ±12.63 | −31.92 | 30.27 | 16 (23.9) | 39 (58.2) | 12 (17.9) | 53.00 | −516.62 | 389.63 | −0.27 | 0.028 |
| 3. | FAO | 1,627 ±162 | −83.39 ± 223.78 | −137.97; −28.80 | 0.539 | −3.46 ± 12.12 | −32.16 | 29.98 | 17 (25.4) | 39 (58.2) | 11 (16.4) | 51.30 | −522.00 | 355.23 | −0.37 | 0.003 |
| 4. | Mifflin | 1,674 ± 175 | −36.43 ± 214.73 | −88.80; 15.95 | 0.589 | −0.81 ± 11.90 | −28.85 | 32.12 | 13 (19.4) | 41 (61.2) | 13 (19.4) | 49.22 | −457.30 | 384.44 | −0.17 | N.S |
| 5. | Schofield a | 1,620 ± 192 | −90.18 ± 237.91 | −148.22; −32.15 | 0.495 | −3.93 ± 12.84 | −33.26 | 27.60 | 20 (29.9) | 36 (53.7) | 11 (16.4) | 54.54 | −556.49 | 376.12 | −0.38 | 0.003 |
| 6. | Schofield b | 1,601 ± 175 | −108.84 ± 229.66 | −164.85, −52.82 | 0.518 | −5.01 ± 12.31 | −33.32 | 27.47 | 23 (34.3) | 34 (50.7) | 10 (14.9) | 52.65 | −558.98 | 341.31 | −0.47 | <0.001 |
| 7. | Müller a | 1,854 ± 154 | 143.44 ± 216.83 | 90.55; 196.33 | 0.574 | 10.09 ± 13.35 | −22.58 | 48.26 | 3 (4.5) | 29 (43.3) | 35 (52.2) | 49.71 | −281.56 | 568.43 | 0.66 | <0.001 |
| 8. | Müller b | 1,859 ± 163 | 148.93 ± 217.07 | 95.99; 201.88 | 0.574 | 10.37 ± 13.35 | −22.73 | 48.15 | 3 (4.5) | 30 (44.8) | 34 (50.7) | 49.76 | −276.53 | 574.39 | 0.69 | <0.001 |
| 9. | Lorenzo | 1,634 ± 168 | −76.27 ± 213.49 | −128.34; −24.19 | 0.593 | −3.16 ± 11.57 | −31.33 | 29.41 | 19 (28.4) | 40 (59.7) | 8 (11.9) | 48.94 | −494.71 | 342.18 | −0.36 | 0.005 |
| 10. | Korth | 1,864 ± 179 | 153.77 ± 213.62 | 101.67; 205.88 | 0.596 | 10.54 ± 13.13 | −19.77 | 48.08 | 3 (4.5) | 29 (43.3) | 35 (52.2) | 48.97 | −264.91 | 572.46 | 0.72 | <0.001 |
| 11. | Weijs | 1,828 ± 185 | 117.40 ± 214.56 | 65.06; 169.74 | 0.595 | 8.34 ± 13.07 | −22.31 | 47.01 | 5 (7.5) | 34 (50.7) | 28 (41.8) | 49.19 | −303.14 | 537.95 | 0.55 | <0.001 |
| 12. | Frankenfield a | 1,806 ± 165 | 95.61 ± 223.52 | 41.09; 150.13 | 0.542 | 7.21 ± 13.34 | −26.33 | 44.02 | 5 (7.5) | 36 (53.7) | 26 (38.8) | 51.24 | −342.48 | 533.71 | 0.43 | 0.001 |
| 13. | Frankenfield b | 1,830 ±168 | 120.38 ± 218.49 | 67.09; 173.68 | 0.569 | 8.64 ± 13.20 | −23.76 | 45.60 | 4 (6.0) | 33 (49.3) | 30 (44.8) | 50.09 | −307.86 | 548.63 | 0.55 | <0.001 |
| 14. | De La Cruz | 1,715 ± 199 | 4.51 ± 232.29 | −52.15; 61.17 | 0.529 | 1.61 ± 13.12 | −30.38 | 33.21 | 11 (16.4) | 38 (56.7) | 18 (26.9) | 53.25 | −450.78 | 459.80 | 0.02 | N.S |
| 15. | Willis | 1,706 ± 191 | −3.90 ± 228.08 | −59.53; 51.74 | 0.539 | 1.13 ± 12.82 | −30.49 | 33.11 | 11 (16.4) | 38 (56.7) | 18 (26.9) | 52.28 | −450.93 | 443.13 | −0.02 | N.S |
| 16. | Huang | 1,795 ± 140 | 84.78 ± 212.20 | 33.20; 136.54 | 0.603 | 6.62 ± 12.77 | −22.93 | 45.01 | 6 (9.0) | 34 (50.7) | 27 (40.3) | 48.64 | −331.13 | 500.69 | 0.40 | 0.002 |
| 17. | De Luis | 1,698 ± 188 | −12.17 ± 234.02 | −69.25; 44.92 | 0.509 | 0.70 ± 13.12 | −30.99 | 32.06 | 15 (22.4) | 34 (50.7) | 18 (26.9) | 53.65 | −470.84 | 446.51 | −0.05 | N.S |
| 18. | Roza | 1,605 ±150 | −105.23 ± 215.38 | −157.77; −52.70 | 0.582 | −4.78 ± 11.43 | −32.40 | 27.26 | 21 (31.3) | 40 (59.7) | 6 (9.0) | 49.37 | −527.37 | 316.91 | −0.49 | <0.001 |
| 19. | Bernestein | 1,312 ± 108 | −397.86 ± 222.79 | −452.20; −343.52 | 0.562 | −22.04 ± 9.53 | −45.38 | 4.69 | 61 (91.0) | 6 (9.0) | 0 (0.0) | 51.07 | −834.54 | 38.82 | −1.79 | <0.001 |
| 20. | Owen | 1,428 ± 86 | −281.85 ± 228.18 | −337.51, −226.19 | 0.557 | −14.98 ± 10.80 | −38.91 | 16.72 | 50 (74.6) | 16 (23.9) | 1 (1.5) | 52.31 | −729.09 | 165.39 | −1.24 | <0.001 |
| 21. | Livingston | 1,710 ± 265 | −180.36 ± 221.18 | −234.31; −126.41 | 0.550 | −9.19 ± 11.18 | −36.63 | 21.09 | 32 (47.8) | 32 (47.8) | 3 (4.5) | 50.70 | −613.86 | 253.15 | −0.82 | <0.001 |
| 22. | Lazzer | 1,598 ± 152 | −92.66 ± 211.20 | −144.18; −41.15 | 0.604 | −4.05 ± 11.50 | −28.81 | 31.13 | 18 (26.9) | 44 (65.7) | 5 (7.5) | 48.41 | −506.61 | 321.28 | −0.44 | 0.001 |
| 23. | Ikeda | 1,507 ± 137 | −202.93 ± 217.27 | −255.92; −149.93 | 0.574 | −10.55 ± 10.83 | −37.38 | 20.18 | 34 (50.7) | 31 (46.3) | 2 (3.0) | 49.81 | −628.78 | 222.93 | −0.93 | <0.001 |
CI = confidence interval; FAO= ; LoA = limits of agreement; REE = resting energy expenditure; WHO = World Health Organization. 1Proportion of people with difference from measured REE < 10% indicating under-prediction. 2Proportion of people with difference from measure REE between 90 and 10% indicating accurate prediction. 3Proportion of people with difference form measured REE >10% indicating over-prediction 4P-value for one sample t-test. a and b, superscripts stands for two versions of the equations shown in the appendix. |
||||||||||||||||
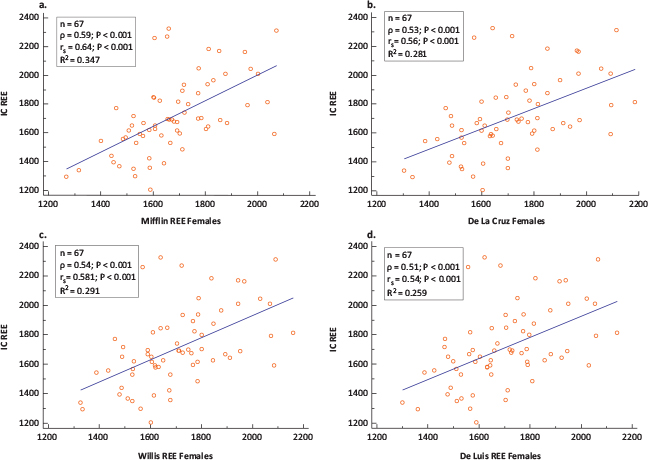
FIG 3. Scatter Plots and Correlation coefficients (ρ =Pearson’s coefficient; rs =Spearman’s Rank Order Coefficient) of Measured Versus Predicted REE in (a) IC and Mifflin, (b) IC and De La Cruz, (c) IC and Willis and (d) IC and De Luis Equations in Females (n = 67).
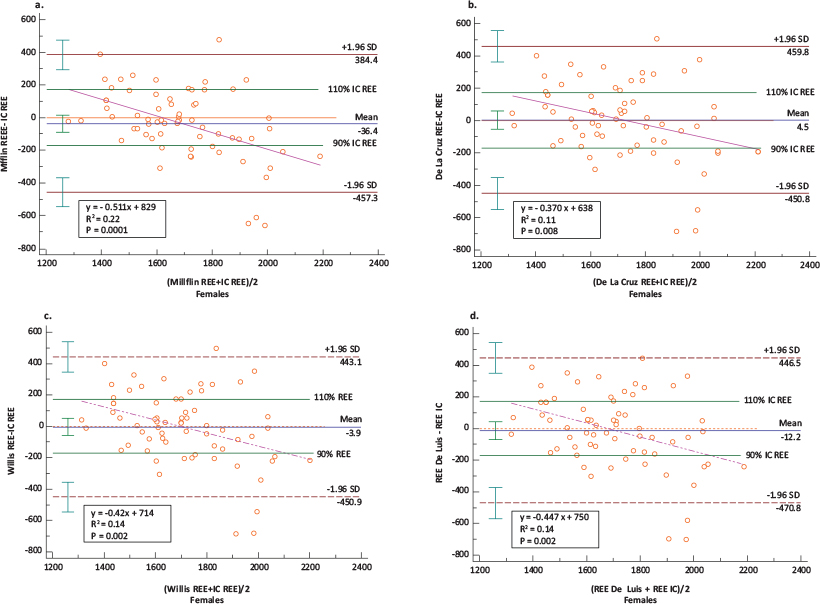
FIG 4. Bland–Altman Plots: Differences in the Measurements of REE Using: (a) IC and Mifflin, (b) IC and De La Cruz, (c) IC and Willis and (d) IC and De Luis Equations in Females (n = 67).
From a practical point of view, De La Cruz in males and Mifflin in females can be used in clinical settings where IC is not available. Both equations demonstrated the best prediction accuracy at the individual level with the least bias.
This study aimed to provide preliminary data regarding the validity and accuracy of a large number of predictive equations for estimating the REE, compared with IC, in treatment-seeking Arab adults with overweight or obesity. Two major findings were revealed.
The first finding of this study is that most predictive equations, especially the more popular equations, such as Harris Benedict,46,47 FAO,40 Müller,23 Schofield,22 Owen19,35 and others, do not seem to be suitable for accurately estimating REE. However, these equations are used by default within different populations—such as ours—to estimate REE. We speculate that several factors may contribute to the invalidity of the most commonly used equations, which we tested amongst our population. Firstly, these equations have mostly been validated for developed populations in Western countries (United States and Western Europe). Secondly, they were developed for use on healthy groups (i.e. those unaffected by obesity or overweight issues).14,46 Finally, ethnicity may be another variable that warrants consideration in relation to equation validation and represents a potential bias.48 In fact, to the best of our knowledge, no equations specifically derived for overweight or obese Arab populations have been validated and this may be the reason for these discrepancies.
Based on our main findings, five equations—namely the WHO (males),40 Del La Cruz (males and females),29 Mifflin (females),21 Willis (females)32 and De Luis (females)31 equations—were shown to have the least bias in estimating REE when compared with the IC measurements. Between genders, the best-performing equation in terms of accurate prediction and percentage bias for estimating REE was the De La Cruz equation in males (accurate predictions: 68.2%; bias: −19.52 kcal/day; % bias: −0.22 ± 9.38% with no systematic bias) and the Mifflin equation in females (accurate prediction: 61.2%; bias: −36.43 kcal/day; %bias: −0.81 ± 11.90% with no systematic bias). The observed percentage bias for Mifflin in females reveals higher accuracy than previously reported.27,49 From a clinical point of view, the identified over- or underestimation in terms of mean bias, percentage bias and the SD or LoA seems to be insignificant in the short term. However, the relatively big SD amounting to 200 kcal/day might have an impact over time, as reported in previous studies.46
We emphasise that it was difficult to compare our findings with other previously published studies on similar populations from Arab-speaking countries. In fact, as far as we are aware, there is only one study that has tested the validity of REE predictive equations compared with values measured by IC.17 However, the sample studied was composed of young Arab females not clearly overweight or affected by obesity and not from a clinical setting (general population).17 In addition, the tool used to measure REE (i.e. Fitmate) is not purely an IC device, since it utilises a fixed value of RQ set equal to 0.85 in the calculations.50,51 Therefore, it does not consider VCO2 and tends to underestimate REE when RQ is effectively between 0.85 and 1.00, and tends to overestimate it if RQ is between 0.70 and 0.85.50,51
The clinical implications of our findings are, firstly, the need to raise awareness in weight-management health providers that the most popular predictive equations based on age, gender, height and weight (Harris Benedict, Food and Agricultural organization [FAO]) do not seem to be particularly reliable in estimating REE in Arab patients and cannot be used by default in a clinical setting. Secondly, our results reveal the availability of only two predictive equations based on weight, gender and age, which are easy and simple to use. This may be of clinical value. This is fortunate, as measuring weight is easy and free, and does not rely on costly specialist tools. However, future research in this field should be focused on the need to develop valid equations to predict accurately REE in this population (i.e. Arab-speaking countries).
Our study has certain strengths. Firstly, we used IC for measurement of REE, which is considered a validated tool for this purpose. Secondly, to the best of our knowledge, this study is the first to assess the validity of several predictive equations for REE in treatment-seeking Arab adults with overweight or obesity in the Arab region. Thirdly, our sample comprised both males and females, treated in a real-world clinical setting. Finally, the inclusion of a large number of REE predictive equations based on age, gender, height and weight is considered a further strength of the study.
However, the study has certain limitations. Firstly, our results must be interpreted with caution, because they may not apply to patients treated in other settings (i.e. inpatients, pharmacotherapy or bariatric surgery patients). Secondly, we did not assess eating habits (quality and quantity) in the days prior to the REE measurement, although this may influence the RQ of the patient.50,51 Finally, the small sample size of our study should also be considered another limitation.
IC remains the preferable method for REE measurement. However, we suggest that the De La Cruz equation in males and the Mifflin equation in females exhibit the best performance in terms of accuracy and bias. Accordingly, these two equations can be best used for the estimation of REE in treatment-seeking Arab adults with overweight or obesity of both genders.
All authors claim authorship and have approved and made substantial contributions to the conception, drafting and final version of this article. The study was designed by ME, while LI conducted the statistical analysis. HT, DK and DE collected data. ME and LI wrote the manuscript.
The authors received no funding.
There is no conflict of interest to report.